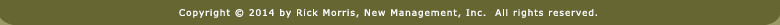The Birthday Game Explained
As I mentioned, this game works because of the fact that it's based on binary math. In binary math you are only allowed to use two numerals: a zero and a one. That's it.
This is such a departure from our traditional base-ten system that it's a bit confusing at first. Nonetheless, with just a brief explanation, you'll be a base-two pro.
Why base-ten works
The reason base-ten works the way it does is because we have ten different numerals we can place in any given column. Therefore, we are able to make 27 by putting a 2 in the ten's column and a 7 in the one's column.
Again, this is so ingrained in our thinking that we forget how confusing the whole thing is to young students as they first learn about it. In fact, you may feel like a kid yourself in just a moment as I move on to why base-two works. (Unless you're a total math-head, that is.)
Why base-two works
Base-two, on the other hand, does not have that much flexibility. You wouldn't, for example, be able to make 27 the same way because you don't have a symbol for 2 or a symbol for 7. You only have a 0 and a 1.
If it helps, think of base-ten as a dimmer switch and base-two as a light switch.
With base-ten, I set the ten's column dimmer switch down to a value of 2 and set the one's column dimmer switch all the way up to a value of 7.
With base-two, I can only turn on the column--by putting a 1 in it--or turn it off--by putting a 0 in it. Thus, I'm going to need to create columns of different values in order to create different numbers.
Let's start with the first column--the one's--and then add more as we need them.
To make the number zero, I place a 0 in the one's column.

To make the number one, I place a 1 in the one's column.

So far, so good. But now we're out of options. We can't do anything else with the one's column but "switch it on" or "switch it off." We need a new column.
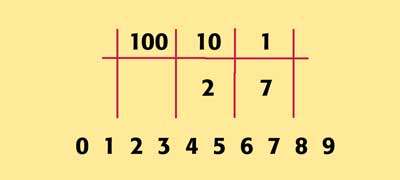
That's right. We add a two's column. This enables us to make the number two by switching on the two's column...
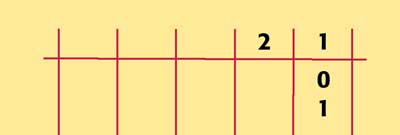
...and switching off the one's column.
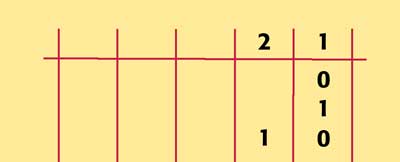
(I know it looks like a 10, but that's base-ten thinking.)
To make the number three, you need a 2 and a 1. So, you switch on both columns.
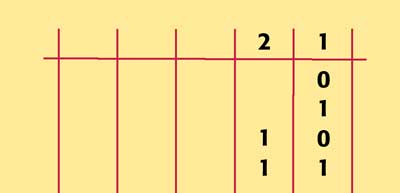
And, once again, we need a new column, the four's. With the four's column in place, we can now make the number four. The four's column is "on" and the other two columns are "off." The number five is made by switching on the four's and one's columns and switching off the two's. To make the number six, you switch on the four's and two's columns and switch off the one's column. (Starting to fell like a befuddled kindergartener?) To make the number seven, you switch on all three columns because 4+2+1 = 7.
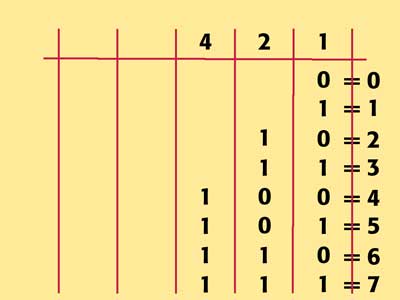
Wow. Look at all of those patterns in the columns.
One thing my students really took to heart was that math is nothing more than patterns and relationships. Everything else? Just details.
Anyway, back to building numbers using base-two.
Uh-oh. We've now used up all of the columns which means we need a new one. We need to add an eight's column. And when those columns are all filled up we're going to need a sixteen's column. (When you go back to look at the Birthday Game cards, notice that the numbers in the upper left-hand corner of each card is actually the name of the columns we've created. Which leads us back to how to make 27 in a base-two system.
Using only the numbers 16, 8, 4, 2, and 1, we realize that 27 = 16+8+2+1.
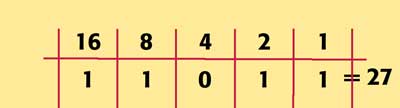
That's why you'll find a 27 on those four birthday cards. You need that column switched on to make 27. However, you won't find it on the birthday card that has a 4 in the upper left-hand corner. You don't need a 4 to make 27. You just need the other numbers.
And that's why the Birthday Game works the way it does. You can figure out any number from 1 through 31--how convenient since we are talking birthdays--by merely asking a student if he sees his birthdate on each card. "Yes" he does? Switch on that column. "No" he doesn't? Switch it off. Add the columns you switched on and you'll have the student's birthdate.
Now that you know how it works, it all makes sense. To your students, though, it's going to seem like voodoo.